小新是直男的概率有多少，难道不应该是100%吗？！

一条微博引发的思考

两周前，我们的微博组发布了这样的一条科技资讯：

就在小新窃以为人工智能之光即将照亮我们FFF团的前进道路之时，一名读者的评论成功引起了小新的注意：

假若数据属实，那么实际美国同性恋人口占总人口不到3.8%（LGBT还包括了双性恋和跨性别者）。根据这样的人口情况，当样本量稍大时，直接猜测对方是直男直女的概率，确实应该比96%还要大。

然而小新并不满足于此，窃以为人工智能和这般押宝式的耍赖猜测会不一样，便询问了学界的朋友。其实，这种问题其实很常见，它反映的是当下许多研究中“统计显著”的错误。

“人工智能也应用到了生物医学领域。有团队用深度学习比对数千片癌细胞切片来预测癌症。但这类研究里，哪怕很高的正确率也没有说服力。”

“因为普通人患癌症的概率本来就微乎其微，总体本身有很高的阴性（正常）比例，很低的阳性（癌症）比例。这种分布极度不均的总体，忽视实际的分布情况，宣称p值小到了多少，有百分之多少的成功率，还是会有很多假阳性的现象。”

“基佬算法”是怎样炼成的

怎样从随机事件中找出想要的那一部分，是一个很古老的问题。

哲学家和统计学家们已经为此奋斗了数个世纪，并取得了不小的成果。这一问题的关键在于演绎逻辑和归纳逻辑的划分。

科学是一项归纳推理的活动，我们从物质世界中观察现象，归纳出一般性原理。但归纳永远是不完善的——即使经典如牛顿力学，也被量子力学颠覆，被限制在了低速条件下。

你永远不知道世界上有没有白乌鸦，直到你发现了一只。

而演绎逻辑则要容易的多：先假定一个原理的正确性，推断后果是什么，再将推断结果与实际结果比较。如果相符，就认为这一原理是对的。

假设gay能通过某种面部特征反映，就先用“基佬算法”抓到这个面部特征，再用人脸验证。如果具有这个特征的男人确实都是gay，就认为“基佬算法”是对的，否则就是错的。

（并不科学的配图）

实际测试中，肯定会出现算法有时灵验有时不灵验的情况。为了决定到底用不用“基佬算法”的一类问题，我们早在20世纪初就形成了这样一种惯例：将问题转化为仅运用演绎推理的问题，从而避免归纳。即“统计显著性检验”。

统计显著检验计算的是：假如本来没有真实的效应，却观察到了我们所看见的现象甚至更极端的现象，这样的概率有多大？

也即：假如一个人不是同性恋，却用算法检测出了同性恋的面相，这样的概率有多大？

这个概率称为p值。显然，p越小，算法的可靠性越高。而对于p值，有一个人为设定的阈值，当某个测试的p<设定值时，我们就认为“基佬算法”可以用，当p>设定值时，我们就认为这套算法行不通，或者叫“接受”和“拒绝”。

P值尽管很强大，尽管广泛运用于涉及统计学的社会科学、生物医学等多领域中，但2005年，斯坦福大学的流行病学家约翰·安尼迪斯的一篇paper《为什么大多数已发表的研究成果是错误的》，把学术界不计其数用p值灌水的paper轰炸得连渣渣都不剩。

为什么“假阳性”这么多

P值虽然给出了正确的答案，却针对了错误的问题。我们需要的，不是一个直男检测出了基佬面相的概率，而是检测出基佬面相时对方真的是基佬的概率。

这两者差别在哪呢？假设10000个男性受试者，其中基佬比为2%。

“基佬算法”有96%的正确率 = 1个直男有4%的概率检测出基佬面相

看起来几率很小吗？请注意：直男在总体中可是占了98%的。

那么，检测出是基佬的直男有：10000×98%×4%=392

鉴于基佬的总数也就200个。哪怕该算法能100%检验出基佬，那么，“基佬面相”的假阳性，并非2%，而是惊人的392/（392+200）=66.2%

发现了吗？在样本分布极度不均的情况下，运用p值的检验可不是那么靠谱的！

何况，在实际情况中我们永远无法知道人群里直男的真实比例，所以，仅仅通过p值，我们很可能永远无法预测假阳性的比例。

这个发现，导致了生物医学界在统计方面的反思。毕竟，不管是流行疾病、遗传病抑或癌症，放到我们整个社会中，发病率可是相当之低。

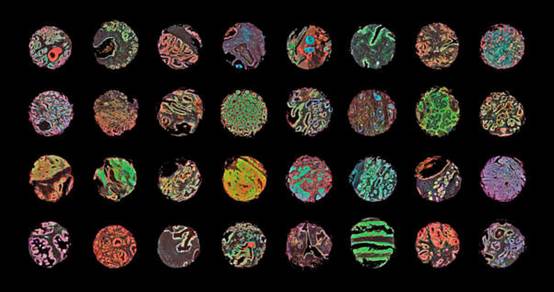
医药科学中的假阳性问题；显微镜下癌症与非癌症的人体组织样本。图片来源：Wellcome Images

人工智能幻觉

许多研究和商业项目宣称能用人工智能“预测”疾病、取向、偏好，很多都是和“相面”一样的比较异同，而不是去探究内在的机理。

尽管这些数字看起来很美，但我们仍需要警惕大数据时代，被巨大商业利益的糖衣所裹挟的“人工智能幻觉”。

只讲数字，不讲原理；只讲相关，不讲因果。其结果是我们很容易把科学研究的权力交由科技公司所掌控。毕竟，在吃瓜群众眼里，两者都是科学。

科学的真正价值在于对探究事物机理的能力，在于对探究过程和分析工具的反思性。人工智能是一条全新的科技树，但科技树基层的这些根，才是人类几百年科学探索所积累的最宝贵财富。